Deep (learning) like Jacques Cousteau - Part 7 - Matrices

(TL;DR: matrices are rectangular arrays of numbers.)

LaTeX and MathJax warning for those viewing my feed: please view directly on website!

I wanted to avoid a picture related to the film franchise!

Me

Last time, we learnt about dot products. We will now finally start talking aobut matrices.

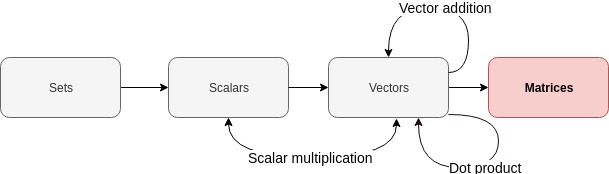
Today’s topic: Matrices - a primer

We know what row vectors and column vectors are from our previous posts.

What would it look like if we were to stack a bunch of row vectors on top of each other? Similarly, what would it look like if we were to put a bunch of column vectors next to each other? Let’s experiment!

Let’s define some row vectors:

\[\boldsymbol{a} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\] \[\boldsymbol{b} = \begin{bmatrix} 4 & 5 & 6 \end{bmatrix}\] \[\boldsymbol{c} = \begin{bmatrix} 7 & 8 & 9 \end{bmatrix}\]

Let’s stack them on top of each other:

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\]

This rectangular array of numbers is an example of a matrix!

Let’s repeat the exercise with the same vectors represented as column vectors:

\[\boldsymbol{a} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\] \[\boldsymbol{b} = \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix}\] \[\boldsymbol{c} = \begin{bmatrix} 7 \\ 8 \\ 9 \end{bmatrix}\]

Putting these column vectors next to each other gives us this:

\[\begin{bmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \\ \end{bmatrix}\]

Looks like another matrix to me!

In fact, our row vectors and column vectors we saw in previous posts live double lives. A row vector goes by another name: “row matrix”. A column vector goes by another name, too: “column matrix”.

Sneaky!

A little bit of notation

As before, we will be following the notation used in Goodfellow, Ian, et al.. We will depict matrices using uppercase, bold font:

\[\boldsymbol{A}\]

Describing the size of a matrix

From the above, we can guess that matrices can be described in terms of rows and columns. How can we describe the number of rows and the number of columns we have in our matrices?

Let’s go back to our previous examples. They both happen to have three rows and three columns. So we have ourselves two 3 x 3 (“three by three”) matrices. The number of rows and the number of columns describe the “size” of our matrix.

Let’s generalise this. By convention, we have \(m\) rows and \(n\) columns in our matrix. Let’s use our matrix \(\boldsymbol{A}\) as an example. We haven’t defined what elements it contains. In fact, all we have said is that \(\boldsymbol{A}\) is a matrix. Whatever the contents of \(\boldsymbol{A}\), it will will have \(m\) rows and \(n\) columns. So \(\boldsymbol{A}\) will be of size \(m \times n\).

Keep it real

Let’s take this a step further. From previous posts, we are working with real numbers so let’s assume that our matrix \(\boldsymbol{A}\) of size \(m \times n\) will contain real numbers. That is, it is a real matrix. How can we depict this using some compact notation?

Remember when we touched on our vectors belonging to some abstract set of all real-valued vectors of similar dimensions when describing the dimensions of a vector? We can say something similar for our real-valued matrix of size \(m \times n\). We can describe this set of all \(m \times n\) real-valued matrices like this:

\[\mathbb{R}^{m \times n}\]

So to show that our matrix \(\boldsymbol{A}\) belongs to the set of all \(m \times n\) matrices that are made up of real numbers, we simply say:

\[\boldsymbol{A} \in \mathbb{R}^{m \times n}\]

Going back to our examples above:

• Our real-valued row vectors (a.k.a. row matrices) are members of the set \(\mathbb{R}^{1 \times n}\). That is, they are members of the set of all possible matrices made up of one row and \(n\) columns of real numbers.
• Our real-valued column vectors (a.k.a. column matrices) are members of the set \(\mathbb{R}^{m \times 1}\). That is, they are members of the set of all possible matrices made up of \(m\) rows and one column of real numbers.
• Our real-valued square matrices are members of the set \(\mathbb{R}^{m \times n}\) where \(m == n\). That is, they are members of the set of all possible real matrices that have the same number of rows as they have columns.

Not too bad, right?

How can we create matrices in R?

Stack those vectors

One way is to simply rbind and cbind vectors. Let’s define 3 vectors and rbind them (i.e. stack them row-wise):

a <- c(1, 2, 3)
b <- c(4, 5, 6)
c <- c(7, 8, 9)

A <- rbind(a, b, c)

print(A)

##   [,1] [,2] [,3]
## a    1    2    3
## b    4    5    6
## c    7    8    9

We have ourselves a matrix!

print(class(A))

## [1] "matrix"

Let’s now stack them column-wise by using cbind on our vectors:

A <- cbind(a, b, c)

print(A)

##      a b c
## [1,] 1 4 7
## [2,] 2 5 8
## [3,] 3 6 9

It’s a matrix!

print(class(A))

## [1] "matrix"

Use the matrix function

The “usual” way to create a matrix would be to pass some vector or list into the matrix function and specify its dimensions. For example, if we want to use the values passed into the matrix function to create a 3x3 matrix by using the values in a column-wise manner, we can do this:

matrix(1:9, nrow=3, ncol=3)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

If instead we want to use the numbers in a row-wise manner, then we can use the byrow argument and set it to TRUE:

matrix(1:9, nrow=3, ncol=3, byrow=TRUE)

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

The data types of the elements in the vector or list you pass into the matrix function will be coerced to a single data type following the usual coercion rules. For example, if we use a vector containing a numeric type and a integer type, let’s see what happens:

our_vec <- c(1.0, 1L)
A <- matrix(our_vec, nrow=2, ncol=1)

print(A)

##      [,1]
## [1,]    1
## [2,]    1

From previous posts, we know that the values in our vector have already been coerced by c before the matrix function sees them! So, naturally, we have a matrix of numeric types:

sapply(A, class)

## [1] "numeric" "numeric"

We can even have a character matrix. Not sure why we’d want to create one…but we can!

x <- c("hello", "goodbye")
matrix(x)

##      [,1]     
## [1,] "hello"  
## [2,] "goodbye"

Elements are recycled

Recycling occurs like in vector addition posts. For example, if we try to create a matrix with four elements (2 rows times 2 columns) from a vector with only two elements, this is what we get:

matrix(c(1, 2), nrow=2, ncol=2)

##      [,1] [,2]
## [1,]    1    1
## [2,]    2    2

If the number of elements in our vector is not a multiple or submultiple of the number of rows or columns, we get warned of this fact:

matrix(c(1, 2, 3), nrow=2, ncol=1)

## Warning in matrix(c(1, 2, 3), nrow = 2, ncol = 1): data length [3] is not a
## sub-multiple or multiple of the number of rows [2]

##      [,1]
## [1,]    1
## [2,]    2

Done!

Conclusion

Next time, we’ll talk about matrix addition and introduce some notation we can use to access the individual elements contained within our matrices!

Justin