I have a problem with socks
Let’s learn how to answer the famous probability interview question involving pairs of socks.
There’s a famous interview question I’ve seen on the internet. It goes something like this:
I have 'x' blue socks and 'y' red socks in a drawer.
I take 2 socks from the drawer without looking.
What is the probability that I have drawn a pair of matching coloured socks?
This sort of question might seem mind-bending for those who haven’t spent much time thinking about probabilities. If you are one of those people, I hope to show you an intuitive way to think through such problems.
Let’s simplify the problem
Instead of starting with 10 blue socks and 10 red socks, let’s start with 2 of each.
We will depict the contents of our sock drawer in a matrix. Remember that we will be drawing pairs of socks. The rows in the matrix will represent the first sock chosen in our pair. The columns will represent the second sock chosen in our pair.
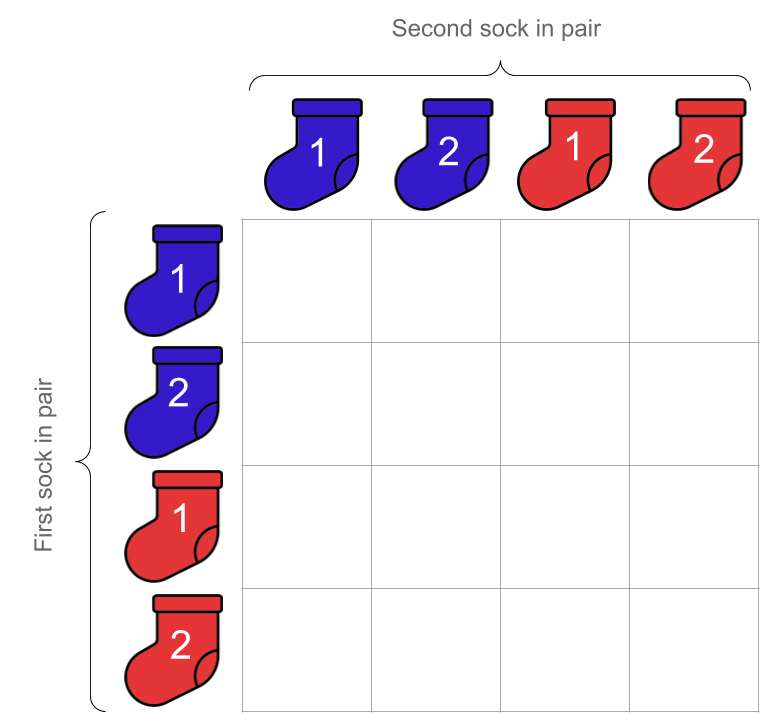
We will depict a particular pair of socks like this:
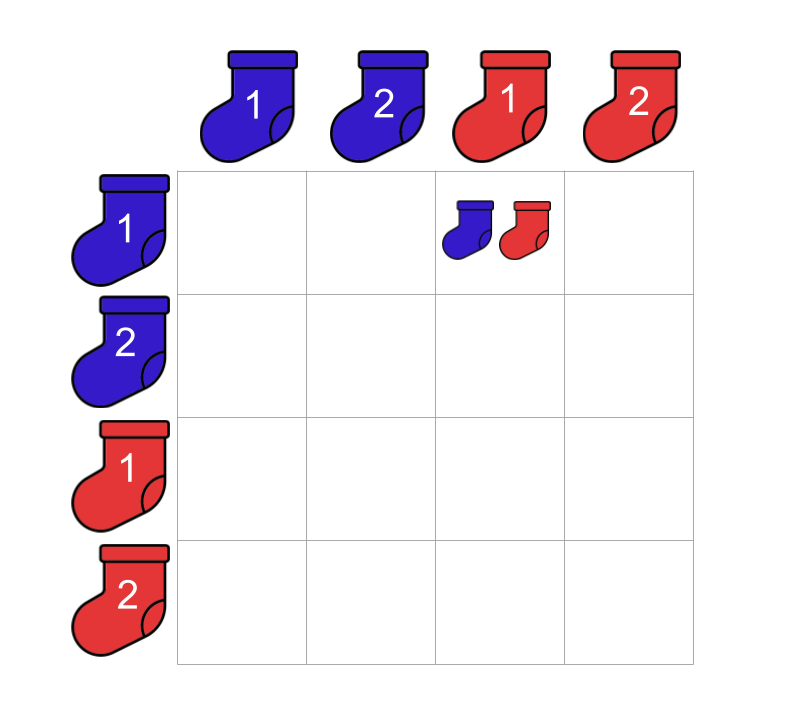
Sampling…no replacement
Say we draw a sock from the draw and it turns out to be the first blue sock (blue-1). We set it aside (i.e. we do not put it back into the drawer). When we go to choose our second sock from the drawer, blue-1 no longer available to us to choose in our little sock universe!
To depict this sampling without replacement, we grey-out the diagonal in our matrix. This is to say that if we have chosen blue-1 as the first sock our pair, blue-1 cannot form the second sock in our pair.
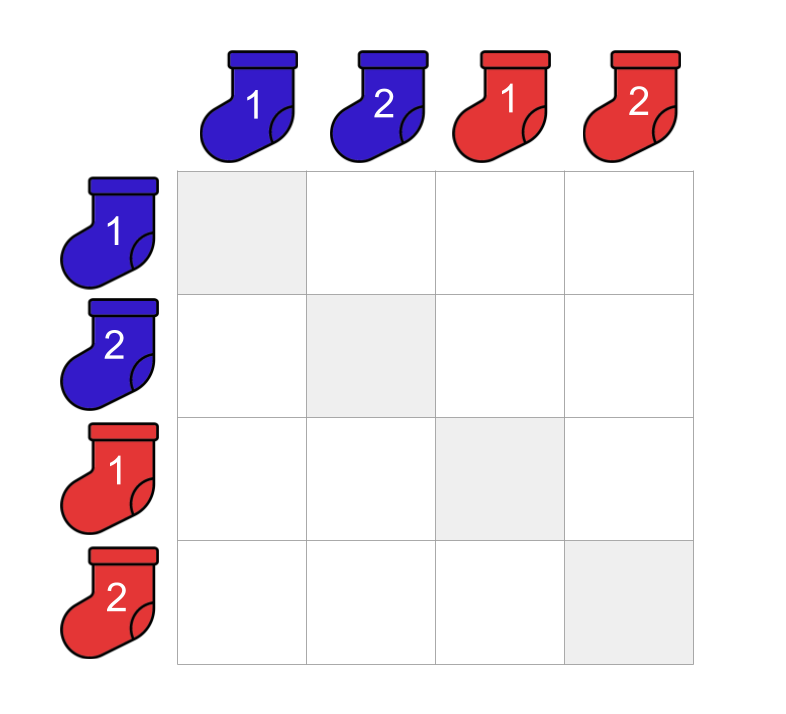
And now for the logic
Let’s walk through some scenarios to gain a better understanding of our problem.
Scenario one: we pick ‘blue-1’
In this scenario, we pick our first sock and it turns out to be blue-1. We set blue-1 aside (i.e. we do not put it back into the draw before picking our second sock). Before choosing our second sock, we stop and think:
“Which socks are available in the drawer at this point?”
This is an easy question to answer! We are down to three choices for the second sock:
- blue-2
- red-1
- red-2
Given that we have chosen blue-1 as our first sock, then what are the pairs we can form using the remaining socks?
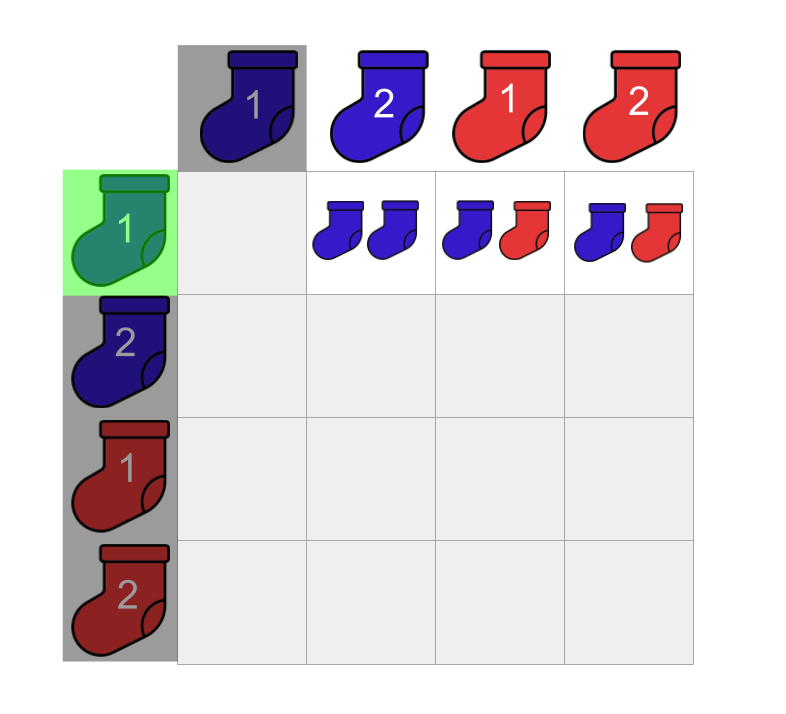
If we count the number of possible pairs we can make in this scenario, we see that we can make 3 pairs!
Scenario two: we pick ‘blue-2’
We hit the ‘reset’ button on our wonderful game and start again.
We choose our first sock. It happens to be blue-2 this time. We set blue-2 aside. We stop and think again:
“Which socks are available in the drawer at this point?”
“This is easy,” you think. We are down to three choices:
- blue-1
- red-1
- red-2
Given that we have chosen blue-2 as our first sock, what are the pairs that can be made with the remaining socks?
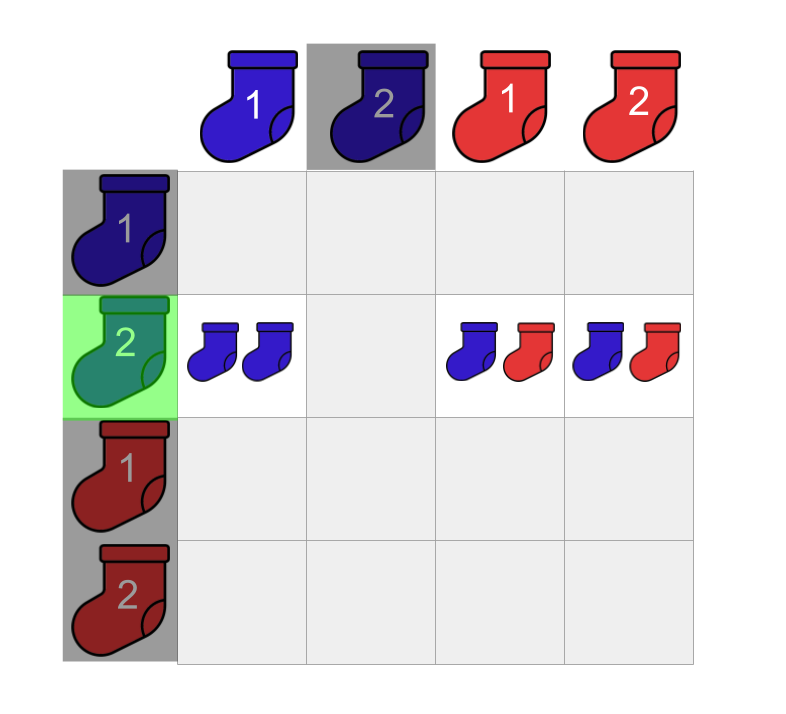
Counting these pairs, we can see that we can also make 3 pairs in this scenario!
Fill the matrix
Let’s repeat the above process until we fill out our matrix.
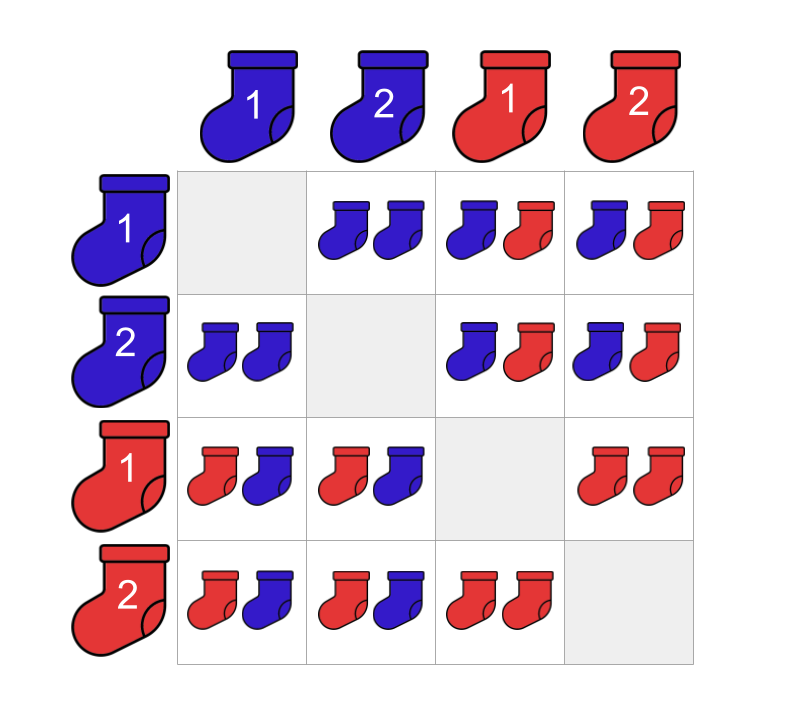
How many pairs can we make in total?
Here, we want to figure out the size of our sock microcosm. If we are simply counting the number of possible pairs that can be made from our 2 blue socks and 2 red socks, we can ignore our ‘matching colours’ restriction. Without this restriction, we can have pairs that have 1 blue sock paired up with 1 red sock. These are the possible pairs we can make:
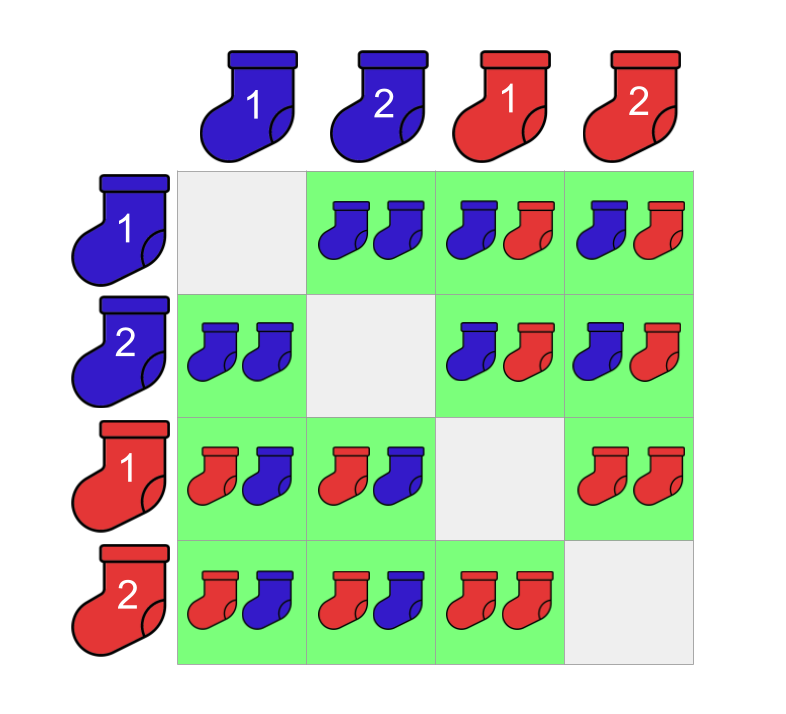
Counting the possible pairs we can make without the ‘matching colours’ restriction, we find that there are 12! This happens to be equal to the number of permutations:
\[P(4, 2) = \frac{4!}{(4-2)!} = 12\]How many matching pairs of socks are there?
Looking at our microcosm of sock pairs, we can count the number of pairs that contain socks of the same colour:
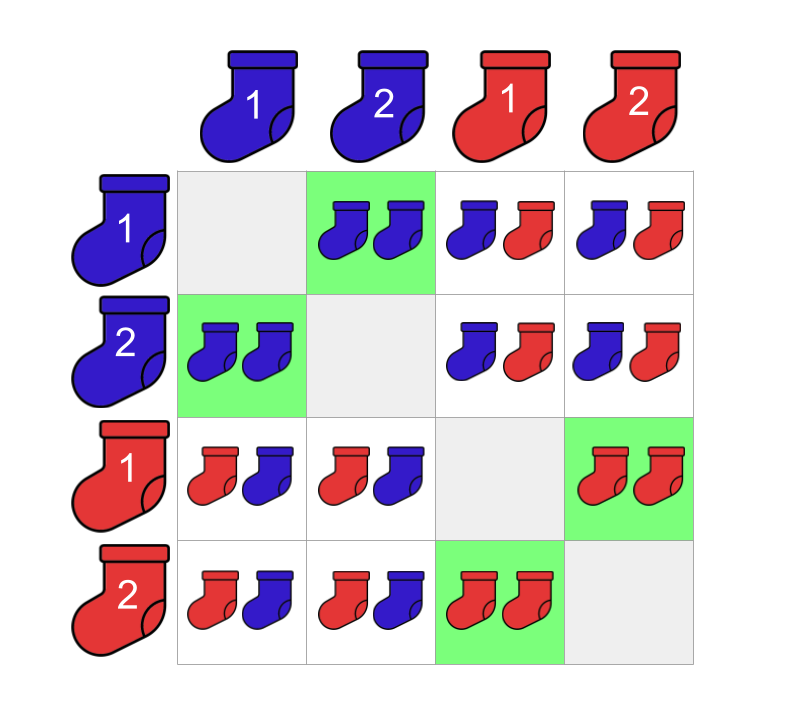
Counting them up, we find that there are 4 matching pairs of socks!
Let’s go a little deeper and think about our matching socks in terms of our sampling without replacement. For our first sock, we have 4 socks to choose from. We take a sock from the drawer and set it aside. For the next sock, 2 cases need to be considered:
Our first sock is blue
If we have drawn a blue sock as our first sock, which of the remaining socks in our drawer could we pick to make a pair of matching socks? We must draw the other blue sock! That is, we are left with only one choice for our second sock that could form a pair of matching blue socks.
Our first sock is red
If our first sock is red, then we must draw the other red sock! That is, we are left with only one choice for our second sock that could form a pair of matching red socks.
It doesn’t matter which sock we choose as our first sock. In order to make a matching pair of socks, we are down to only one choice for the second sock - the remaining sock of the same colour! So for our example, we have:
\[\textrm{4 choices for first sock} \times \textrm{1 choice for our second sock} = \textrm{4 possible matching pairs}\]Take a look at the matrix above and convince yourself that this makes sense!
The big reveal
To answer our initial question, the probability of drawing a matching pair of socks if we were to blindly take two socks without replacement from our drawer is:
\[\frac{\textrm{4 matching pairs}}{\textrm{12 total pairs}} \approx 0.333\]Not bad, right?
What if we increase the number of socks?
Let’s make the problem (seemingly) more difficult. This time we have 100 blue socks and 100 red socks. To solve this, all we have to do is to follow the same logic!
How many total pairs are there?
- For our first sock, we have \(100 + 100 = 200\) total socks to choose from.
- We take one and set it aside.
- We are after the total pairs that we can make from the socks in our drawer. This means that we have \(199\) choices for our second sock.
- Therefore, we have \(200 \cdot 199 = 39,800\) total pairs that can be made from the socks in our drawer.
How many pair of matching socks are there?
- We again have \(200\) choices for the first sock.
- We take note of the colour of the sock and set it aside.
- As we now know the colour of our first sock, we now know how many of the remaining socks we could choose from to create a matching pair of socks! We must have \(100-1=99\) socks to choose from for our second sock.
- Therefore, we have \(200 \cdot 99 = 19,800\) pairs of matching socks.
So what is the probability of drawing a pair of matching socks from this drawer? Here’s the answer:
\[\frac{\textrm{19,800 matching pairs}}{\textrm{39,800 total pairs}} \approx 0.497\]What if we change the proportions of the colours?
In the above examples, we have the same number of blue and red socks in the drawer. What if we make the number of blue socks different to the number of red socks? Let’s say that we now have 100 blue socks and 25 red socks.
How many total pairs are there?
- We start with \(125\) socks in our drawer.
- We take our fist sock and set it aside.
- We have one hundred and twenty-four socks left in our drawer.
- Therefore, we have \(125 \cdot 124 = 15,500\) total pairs.
How many pair of matching socks are there?
- We have 2 cases to consider: the case where our first sock is blue, and the case where our first sock is red.
- If our first sock is blue, then we initially had \(100\) socks to choose from for our first sock. We have the remaining \(99\) blue socks to choose from to form a matching pair of blue socks. Therefore, there are \(100 \cdot 99 = 9,900\) possible pairs of blue socks.
- If our first sock is red, then we have \(25\) socks to choose from for our first sock. We have the remaining \(24\) red socks to choose from to form a matching pair of red socks. Therefore, there are \(25 \cdot 24 = 600\) possible pairs of red socks.
To get the number of pairs of matching socks we can form in this scenario, we simply add the number of matching blue and red pairs:
\[\textrm{number of matching pairs} = \textrm{number of blue sock pairs} + \textrm{number of red sock pairs} \\ = \textrm{9,900 pairs of blue socks} + \textrm{600 pairs of red socks}\]Then what is the probability of drawing a pair of matching socks? Here’s our answer:
\[\frac{\textrm{9,900 pairs of blue socks} + \textrm{600 pairs of red socks}}{\textrm{15,500 total pairs}} \approx 0.68\]Let’s empirically test this
We could simulate the scenario above in Python! Yes, yes yes - there are more efficient ways of doing this. However, I’m trying to explain a concept instead of flexing my engineering muscles so please bear with my verbosity.
The only package we will be using is NumPy. We set the random seed as we will be performing some random sampling!
import numpy as np
np.random.seed(123)
We define the number of socks and the number of times we want to repeat our simulation:
NUM_BLUE_SOCKS = 100
NUM_RED_SOCKS = 25
NUM_TRIALS = 100_000
We create two lists of socks that we will be sampling from.
blue_socks = ['B' for _ in range(NUM_BLUE_SOCKS)]
red_socks = ['R' for _ in range(NUM_RED_SOCKS)]
print(f"blue_socks:\n\n{blue_socks}")
print()
print(f"red_socks:\n\n{red_socks}")
blue_socks:
['B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B']
red_socks:
['R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R']
We create our sock universe by combining the two lists:
all_socks = blue_socks + red_socks
print(f"all_socks:\n\n{all_socks}")
all_socks:
['B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'B', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R']
We write a simple function to draw pairs of socks:
def draw_pairs(num_trials):
trial_results = {}
for trial_num in range(num_trials):
if trial_num % 10000 == 0:
print(f"running trial number: {trial_num}")
trial_results[trial_num+1] = np.random.choice(all_socks, 2, replace=False).tolist()
return trial_results
We write another to calculate the proportion of total pairs that were matching pairs:
def calc_prop_matching_pairs(trial_results):
num_matching_pairs = sum([1 for x in results.values() if x[0] == x[1]])
num_total_pairs = len(results.values())
# of all the pairs we have drawn, what proportion were matching pairs of socks?
prop_matching_pairs = num_matching_pairs / num_total_pairs
print(f"\nprop valid pairs over {NUM_TRIALS:,} trials: {prop_matching_pairs:.2f}")
We then call our functions:
results = draw_pairs(NUM_TRIALS)
calc_prop_matching_pairs(results)
running trial number: 0
running trial number: 10000
running trial number: 20000
running trial number: 30000
running trial number: 40000
running trial number: 50000
running trial number: 60000
running trial number: 70000
running trial number: 80000
running trial number: 90000
prop valid pairs over 100,000 trials: 0.68
We see that our results match. We sit back and smile.
Conclusion
I guess the point of this post was never to show you how to count pairs of matching socks. We have learnt something far more valuable than that!
We have seen that a seemingly difficult problem can be solved by simplifying it. Once we figure out how to solve the simpler problem, we can see whether our logic holds on the more complex problem.
As a bonus, if you’re ever asked this question in an interview, you can smugly tell your interviewer this:
“I know how to answer this question. But shouldn’t you be focusing on the bigger picture?”
See you next time.
Justin
Credit
The sock image used throughout this post is by the user ibrandify from the Noun Project. Thank you!