Statistical significance intuition

An attempt at explaining a difficult concept in a characteristically dense but intuitive way

References (I highly recommend all of these books):

“Statistical methods in online A/B testing” by Georgi Z. Georgiev
“Introductory Statistics and Analytics: A Resampling Perspective” by Peter C. Bruce
“Practical Statistics for Data Scientists” by Peter Bruce, Andrew Bruce and Peter Gedeck
“Reasoned Writing” and “A Framework for Scientific Papers” by Devin Jindrich
“Trustworthy Online Controlled Experiments: A Practical Guide to A/B Testing” by Ron Kohavi, Diane Tang and Ya Xu

I’m going to try to explain what “statistical significance” means, using a fake experiment to test a rates-based metric (the conversion rate). I’ll try not to use much jargon and almost no maths. I might be imprecise. The goal of this post is intuition over precision.

Notes:

• I’ll be ignoring concepts like power, minimum detectable effect, and one/two-tailed tests as they’ll cloud intuition.
• I’ll be using a resampling approach rather than relying on traditional formulae because the resampling approach is more intuitive.

Let’s jump right in!

Python stuff used in this post

import random
import numpy as np
from statsmodels.stats.proportion import score_test_proportions_2indep
from scipy import stats
from numba import njit, prange
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import seaborn as sns

Some settings:

rng = np.random.default_rng(1337) # random number generator using the one true seed
sns.set_style('white')

Set up a fake experiment

Note: We’ll be using absurdly small sample sizes in the following. Again, intuition is the goal.

Let’s say that we have a new search ranking algorithm that we think outperforms our current search ranking algorithm. In our experiment, we have two groups that we’ll be comparing:

• One set of users who are exposed to the search ranking algorithm in production today. We’ll call this the “control group”.
• Another set of users who are exposed to the new search ranking algorithm. We’ll call this the “variant group”.

How do users get into these groups in the first place?

On the random assignment of users to our control and variant groups

We will randomly assign users appearing on our website into our control and variant groups. The key reason why we randomly assign users to our control and variant groups is this:

We want to be confident that the only difference between our two groups is the difference in search ranking algorithms.

What if we were to do this instead?

• Assign users who live in Australia to the control group
• Assign users who live in the USA to the variant group

Now, the differences between our groups aren’t solely the difference in search ranking algorithms. We now have a geographical difference. Users living in Australia might not behave in the same way as users in the USA. The two countries might be different in demographical factors like age.

These differences cloud our ability to measure the “true” degree of outperformance between our algorithms. So let’s stick to random assignments.

How will we measure the performance of each algorithm?

We now have two groups of randomly assigned users who are exposed to different search ranking algorithms.

We need a metric that we can use to call our experiment a success or a failure. Let’s use something familiar to most - the “conversion rate”. We’ll define “conversion” as “a user buying something”.

The conversion rate for a single group in our experiment

For each user in our experiment, there are two outcomes:

• A user converts during our experiment
• A user doesn’t convert during our experiment

We’ll define our conversion rate like this:

\[\text{Control group conversion rate} = \frac{\text{Number of unique converting users in our control group}}{\text{Number of unique users in our control group}}\]

We do the same for our variant group:

\[\text{Variant group conversion rate} = \frac{\text{Number of unique converting users in our variant group}}{\text{Number of unique users in our variant group}}\]

Let’s illustrate our conversion rate. Here is a timeline of an experiment:

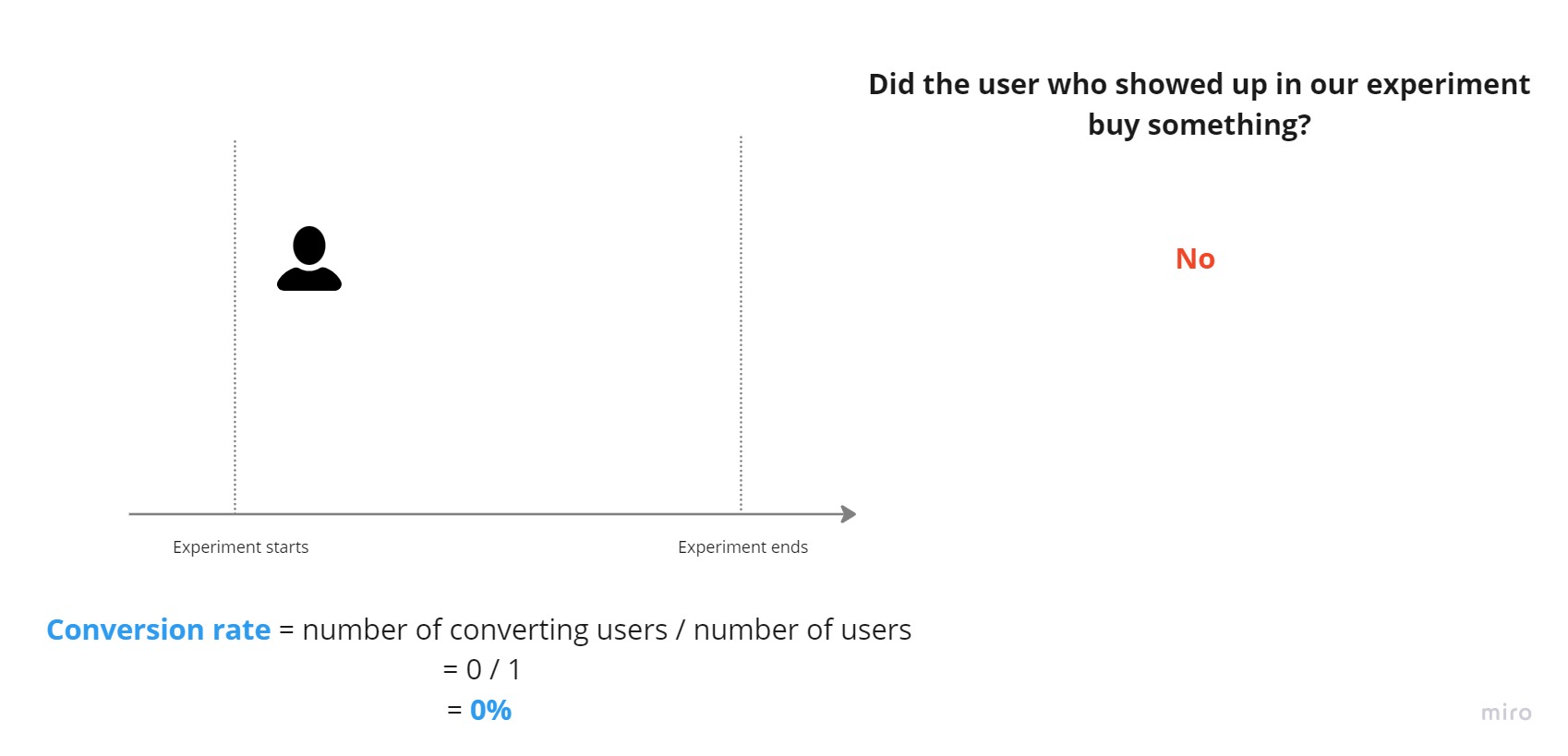
A user shows up in our experiment. They haven’t bought anything yet, so the conversion rate is 0%:

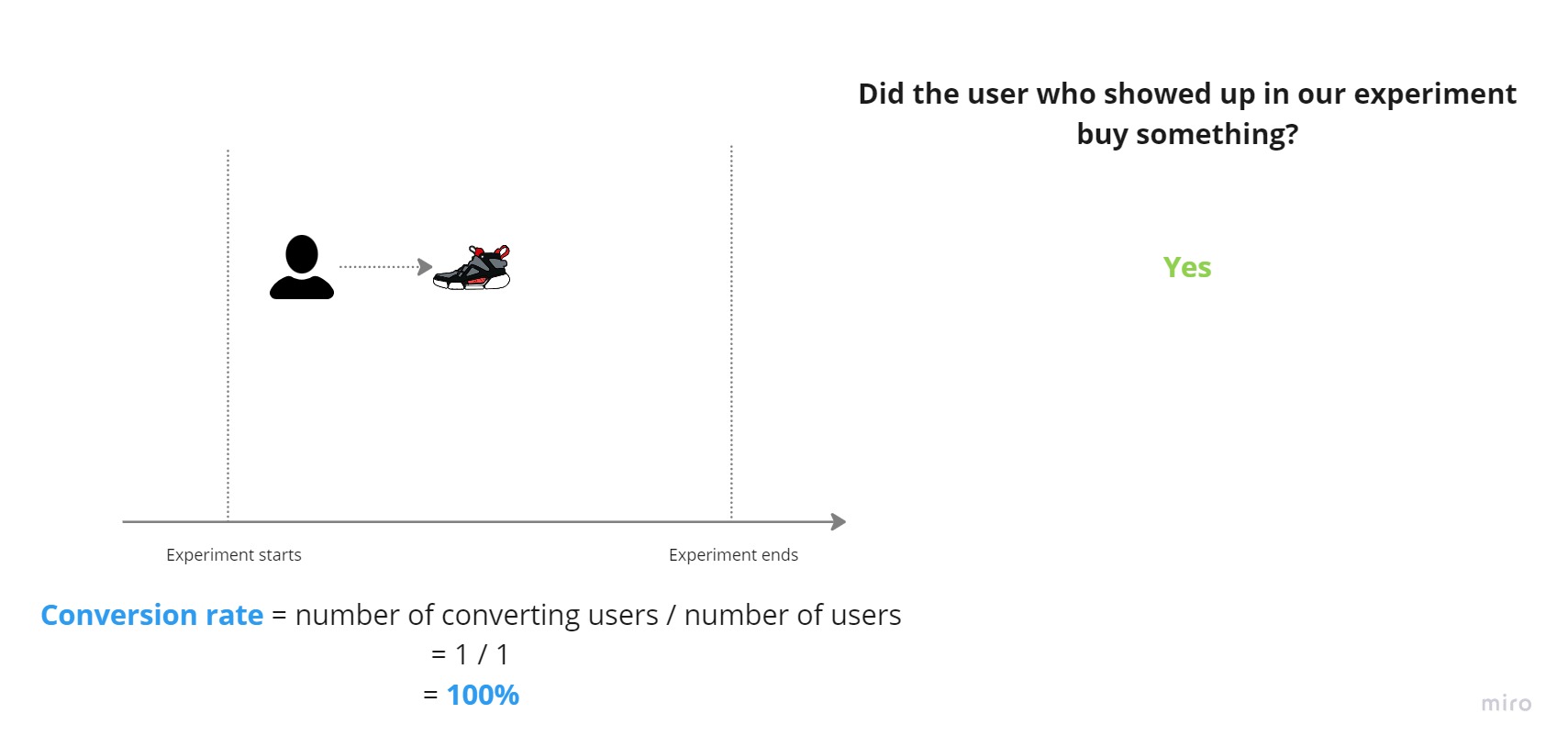
Hooray! The user bought a pair of sweet, sweet sneakers. The conversion rate is now 100%:

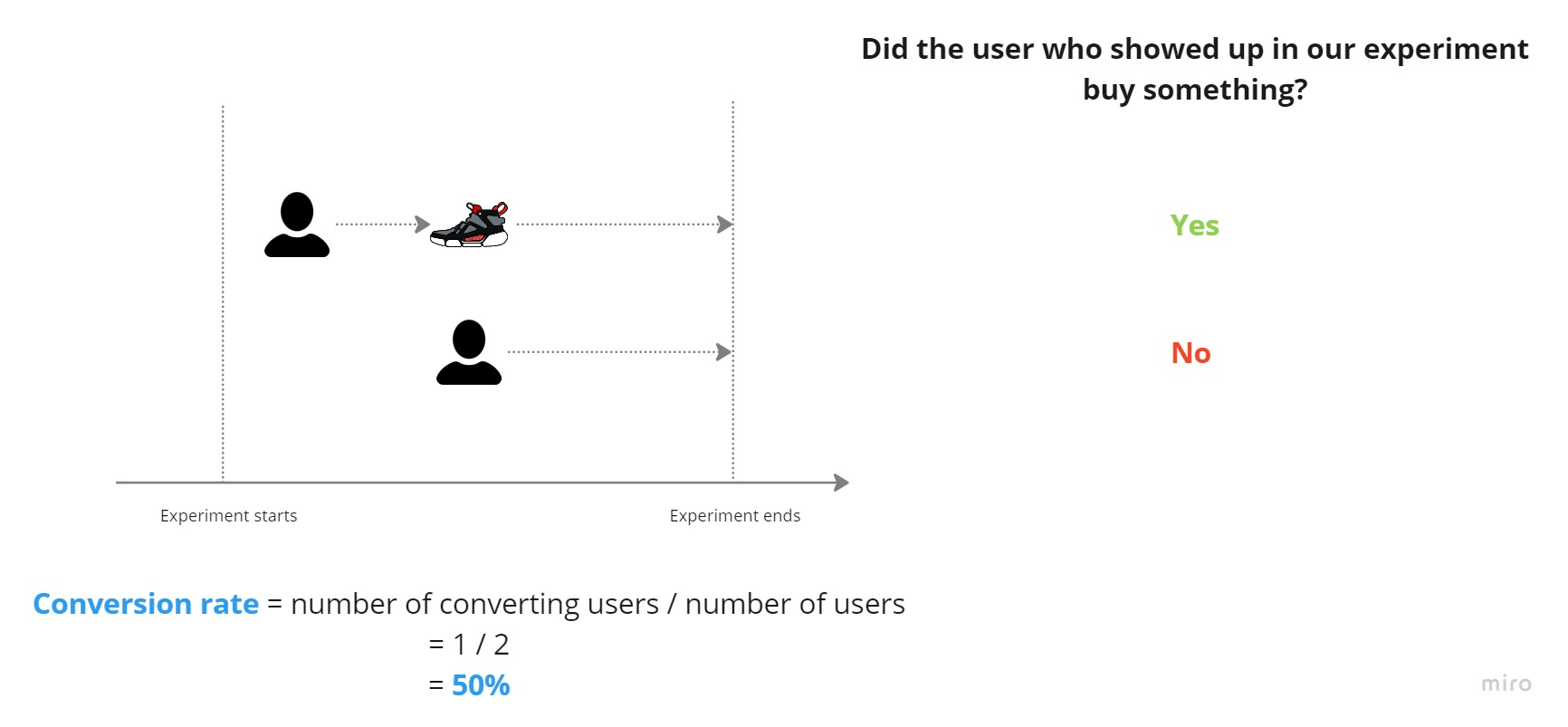
A second user shows up in our experiment. They unfortunately don’t buy anything and the experiment ends. The conversion rate is 50% for the experiment:

How will we measure the “outperformance” of our new algorithm over the existing one?

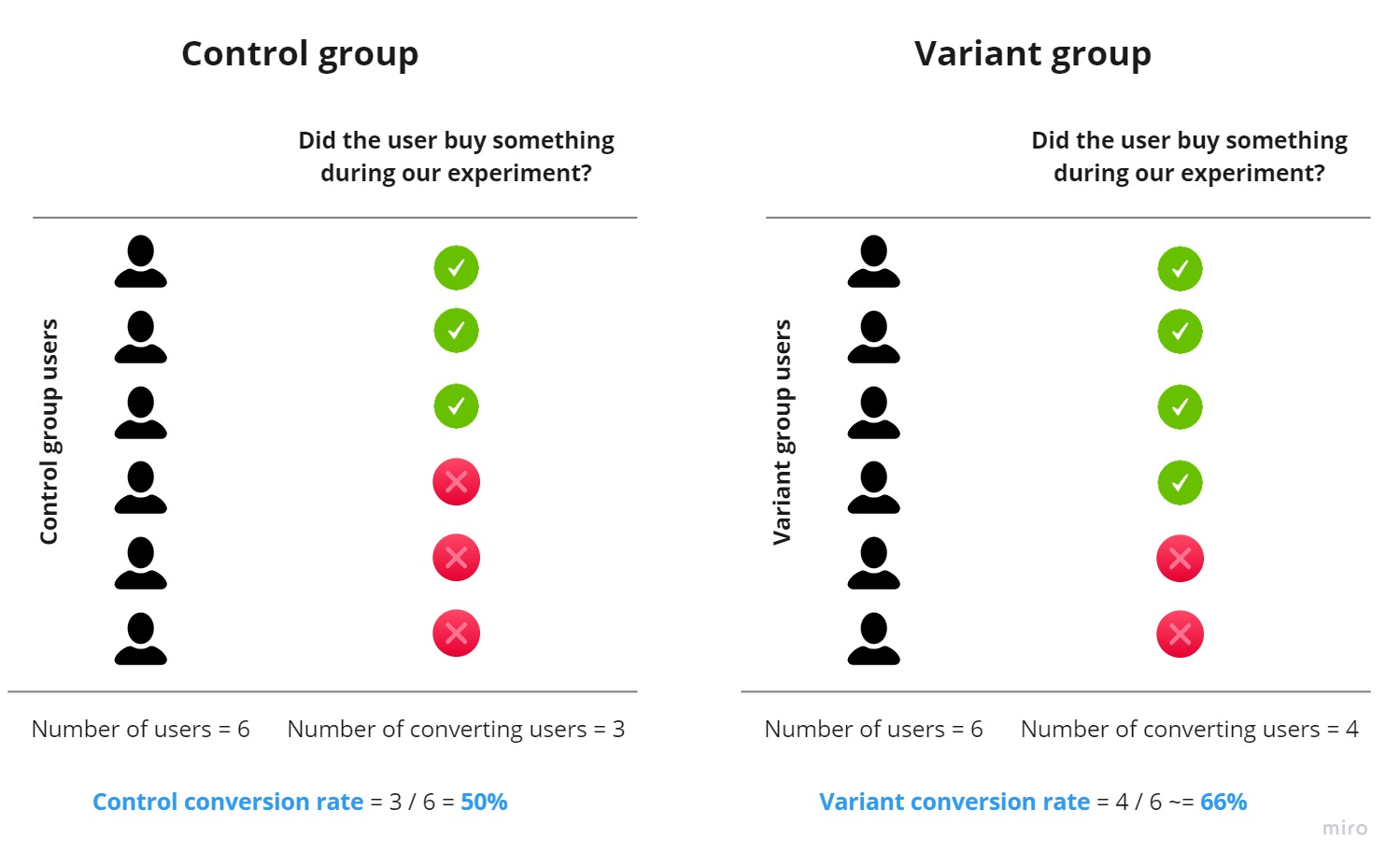
We have two groups with an equal number of randomly assigned users. We now have two conversion rates:

How can we distil these two rates into a single metric that can be used to describe the difference in performance between the two algorithms? That’s easy!

What we’re interested in is the difference in conversion rates between these groups. Let’s calculate the difference in conversion rates in the above scenario:

\[\begin{align*} \text{Difference in conversion rates} &= \text{Variant conversion rate} - \text{Control conversion rate} \\ &\approx 66.7\% - 50.0\% \\ &\approx 16.7\% \end{align*}\]

Wow, a +~16.7% absolute difference to control! That’s a relative change of \(\frac{16.7\%}{50\%} \approx ~33.3\%\)!!!

Is the difference in conversion rates just random noise?

We have a +~16.7% absolute difference in conversion rates. It looks like our variant algorithm performs better! We have a winner! Let’s release this to production. Right? Right?

No! Not yet. Let’s dive head-first into the rabbit hole.

We can’t include all current and all future users in our experiment. That’s impossible! We’re constrained by reality. In our experiment, we’ve only sampled 12 users in total, 6 of whom were randomly assigned to the control group, and 6 of whom were randomly assigned to the variant group.

By only sampling 12 users from a hypothetically infinite group of users, there’s some randomness in which users show up during our experiment. Furthermore, even though we’ve randomly allocated users to the control and variant groups, there’s a naturally random variation in how users behave within each group.

This means our conversion rate measurements are “tinged with randomness”. Oh, beautiful randomness.

Our job is to make an intelligent guess from our limited experiment users whether what we’ve observed is a random blip in outperformance, or whether it could be “true outperformance”.

On our parallel worlds

We have two competing states of the world that describe our observed difference in conversion rates:

We don’t know which state of the world we’re in. We need to infer which state of the world best describes our experiment results.

Our reasoning process

We reason in a reversed way.

We firstly assume we’re in World 1:

We consider our experiment results and how special they are in World 1. We can think of this as answering the question “How out of place are our experiment results if we’re in a world where randomness might have caused our experiment results?”:

If the experiment results are special enough (i.e. they’re rare in a world where randomness might have caused the results we’ve observed), we say that randomness is a poor descriptor of our experiment results. We conclude that there’s good evidence that our variant algorithm performs better than our control algorithm:

If the experiment results aren’t special enough, we conclude that there’s not enough evidence to say that the variant algorithm performs better than the control algorithm:

On quantifying how well randomness explains our results

How can we quantify how special or not special our experiment result of ~16.7% difference in conversion rates really is?

• We could come up with a range of differences in conversion rates caused by randomness alone, and see how extreme our result of ~16.7% difference is.
• To come up with a range of random variation in the difference in rates, we can use simulations by “injecting randomness” into our experiment results!
• We’ll inject randomness into our experiment results by randomly shuffling our users and creating many different control and variant groups. The key is that we’re randomly shuffling our users. It’s like we’re shuffling a deck of cards. This is pure randomness!

Here are our users from the above artificial experiment, indicating whether they converted or didn’t convert during our experiment:

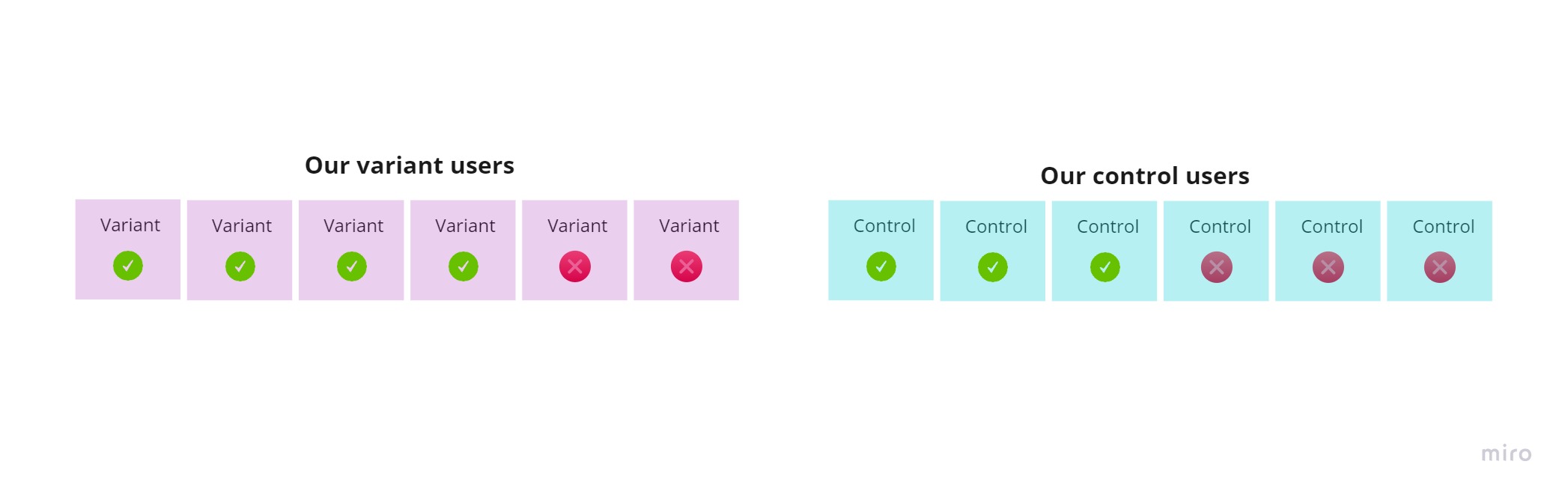
We’re going to chuck our users into a bag. Let’s create our “bag”:

Let’s do the “chucking”:

Let’s randomly shuffle our users:

From here on, we’ll keep only our users’ conversion statuses so that it’s easier to understand:

We’ll take the first 6 users and call this our “simulated variant group created by pure randomness”. We’ll take the next 6 users and call this our “simulated control group created by pure randomness”:

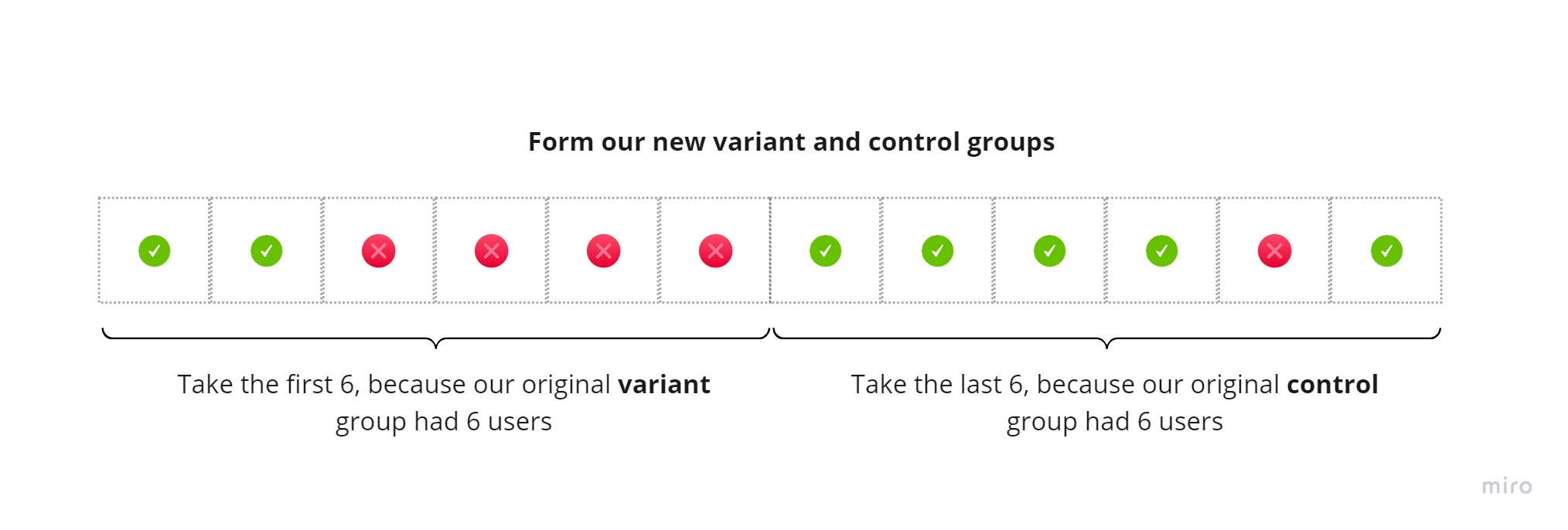
We then calculate our difference in rates between our simulated control and variant groups caused by “pure randomness”:

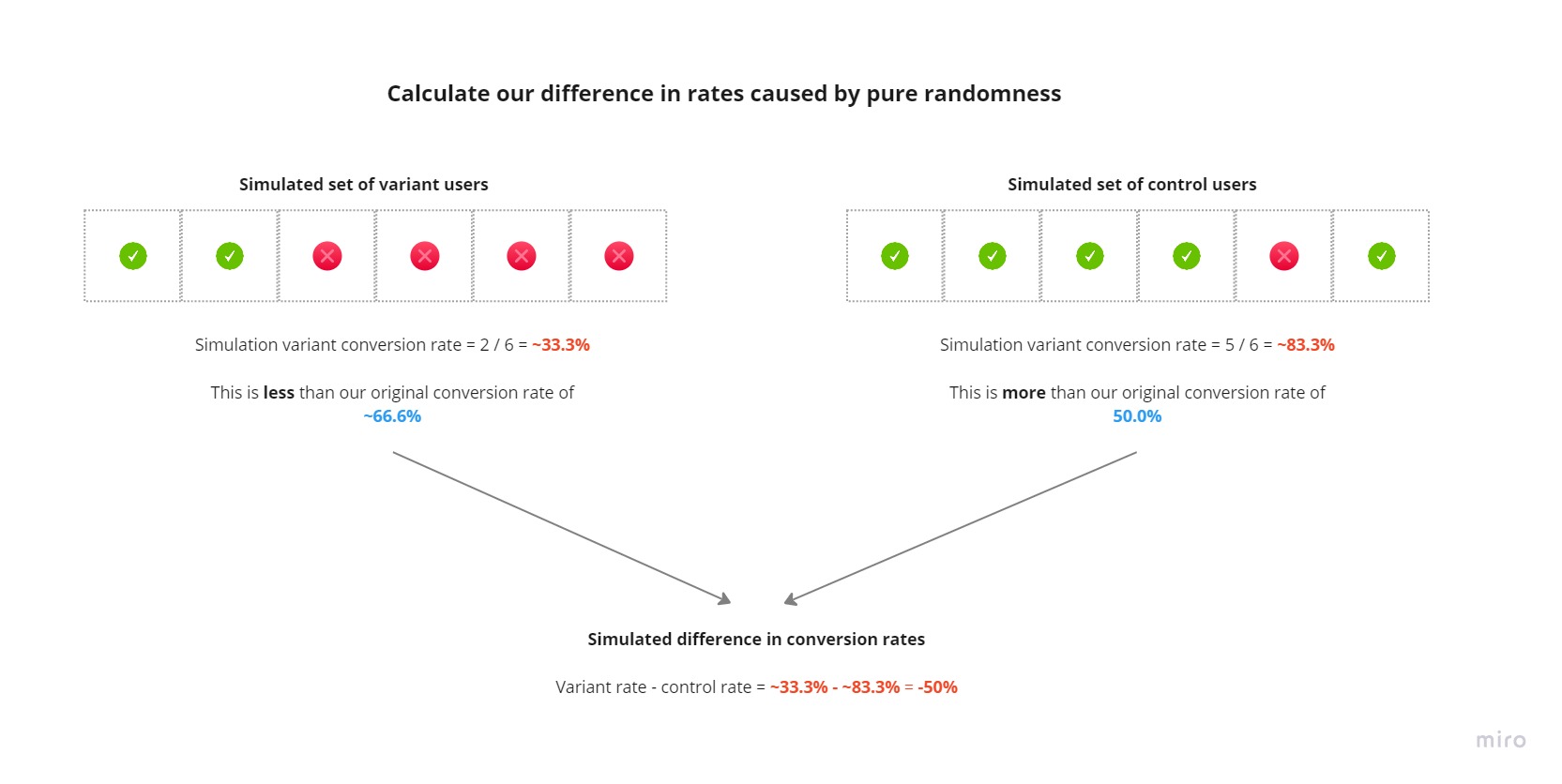
We repeat this process many times to get a distribution of pure randomness and see where our observed difference of ~16.7% lies.

Now, onto Python!

Creating our range of pure randomness in Python

We’ll be using these techniques for the rest of the post.

Let’s create an array that represents users in our control group and whether the user at that position in the array converted or not. We’re dealing with binary outcomes (the user either converts or not):

• A user who converted will be given the value 1
• A user who didn’t convert will be given the value 0

NUM_CONTROL_USERS = 6 # total number of users in control group

We’ll create an array in which each index represents a user in our control group:

control_users = np.zeros(NUM_CONTROL_USERS)

control_users

array([0., 0., 0., 0., 0., 0.])

We’ll set the converting users to 1’s:

NUM_CONVERTING_CONTROL_USERS = 3
control_users[:NUM_CONVERTING_CONTROL_USERS] = 1.0

control_users

array([1., 1., 1., 0., 0., 0.])

What’s our control conversion rate?

control_conversion_rate = control_users.mean()
print(f"control conversion rate: {control_conversion_rate:.1%}")

control conversion rate: 50.0%

We’ll do the same for our variant group users:

NUM_VARIANT_USERS = 6
NUM_CONVERTING_VARIANT_USERS = 4

variant_users = np.zeros(NUM_VARIANT_USERS)
variant_users[:NUM_CONVERTING_VARIANT_USERS] = 1.0

variant_conversion_rate = variant_users.mean()
print(f"variant conversion rate: {variant_conversion_rate:.1%}")

variant conversion rate: 66.7%

The difference in rates we saw in our experiment is this:

observed_diff_in_rates = variant_conversion_rate - control_conversion_rate
print(f"observed difference in conversion rates: {observed_diff_in_rates:.1%}")

observed difference in conversion rates: 16.7%

Very good!

Let’s run one iteration of our simulation. Let’s chuck our control and variant users into a bag:

all_users = np.hstack([control_users, variant_users])

all_users

array([1., 1., 1., 0., 0., 0., 1., 1., 1., 1., 0., 0.])

Let’s randomly shuffle them:

rng.shuffle(all_users)

all_users

array([0., 1., 1., 0., 1., 1., 1., 0., 0., 0., 1., 1.])

We create our simulated control and variant groups:

simulated_control_group = all_users[:NUM_CONTROL_USERS]
simulated_variant_group = all_users[NUM_CONTROL_USERS:]

simulated_control_group, simulated_variant_group

(array([0., 1., 1., 0., 1., 1.]), array([1., 0., 0., 0., 1., 1.]))

What are our simulated conversion rates?

print(f"simulated control conversion rate: {simulated_control_group.mean():.1%}")
print(f"simulated variant conversion rate: {simulated_variant_group.mean():.1%}")

simulated control conversion rate: 66.7%
simulated variant conversion rate: 50.0%

simulated_diff_in_rates = simulated_variant_group.mean() - simulated_control_group.mean()

print(f"simulated difference in conversion rates: {simulated_diff_in_rates:.1%}")

simulated difference in conversion rates: -16.7%

Not quite our result of ~+16.7%, is it?

Let’s do this many times:

NUM_SIMULATIONS = 10_000
simulated_diffs_in_rates = []

for _ in range(NUM_SIMULATIONS):
    rng.shuffle(all_users)
    control_conversion_rate = all_users[:NUM_CONTROL_USERS].mean()
    variant_conversion_rate = all_users[NUM_CONTROL_USERS:].mean()
    simulated_diffs_in_rates.append(variant_conversion_rate - control_conversion_rate)

simulated_diffs_in_rates = np.array(simulated_diffs_in_rates)

Let’s inspect our first 10 simulated difference in rates:

for i, rate in enumerate(simulated_diffs_in_rates[:10]):
    print(f"simulated diff in rates {i+1}: {rate:.1%}")

simulated diff in rates 1: -50.0%
simulated diff in rates 2: -16.7%
simulated diff in rates 3: 16.7%
simulated diff in rates 4: 16.7%
simulated diff in rates 5: 50.0%
simulated diff in rates 6: 50.0%
simulated diff in rates 7: -16.7%
simulated diff in rates 8: -16.7%
simulated diff in rates 9: -50.0%
simulated diff in rates 10: 16.7%

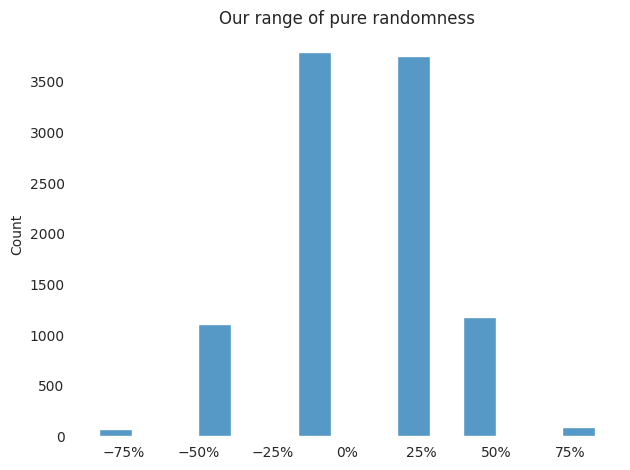
Let’s plot our distribution of pure randomness. This is our distribution of random noise!

Note: we’re dealing with extremely small sample sizes so the distribution ain’t pretty. We’ll be running a large-scale fake example next.

def plot_hist(experiment_results: np.ndarray,
              bins=100,
              observed_rate: float = None,
              title: str = None) -> None:
    sns.histplot(experiment_results, bins=bins)
    if observed_rate:
        plt.axvline(observed_rate, color='r', label='Diff in rates observed in experiment')
        plt.legend(bbox_to_anchor=(0.5, -0.2), loc="lower center")
    if title:
        plt.title(title)
    plt.gca().xaxis.set_major_formatter(ticker.PercentFormatter(xmax=1.0))
    sns.despine(left=True, bottom=True)
    plt.tight_layout()


plot_hist(simulated_diffs_in_rates,
          bins=15,
          title="Our range of pure randomness")

How “special” are our experiment results? On statistical significance

Let’s now infer which world we’re in. Let’s recap our reasoning process:

• If our observed experiment result of ~+16.7% “isn’t special enough”, we’re probably in World 1. This is the world where we assume that our experiment result is probably due to random chance. We conclude that, given our experiment, there’s insufficient evidence to say that our variant algorithm performs better than our control algorithm.
• If our experiment result “is special enough”, then we’re probably in World 2. This is the world where random chance isn’t a good description for our observed experiment result of ~+16.7%. We conclude that, given our experiment, there’s strong evidence to suggest that our variant algorithm performs better than our control algorithm.

Let’s restate our phrases “isn’t special” and “special” in the context of our distribution of random noise:

• If it’s “common” to see an experiment result greater than or equal to ~+16.7% in our distribution of random noise, then our result “isn’t special”. This means that random noise explains our experiment results well.
• If it’s “rare” to see an experiment result greater than or equal to ~+16.7% in our distribution of random noise, then our result is “special”. This means that random noise doesn’t explain our experiment results well.

We can now address the “enough” part of the phrases “isn’t special enough” and “is special enough”. The most common threshold of “specialness” used is 5%. What does this mean in our context?

• If more than 5% of our randomly generated differences in conversion rates are greater than or equal to our observed experiment result of ~+16.7%, then we say that our experiment result “isn’t special enough”.
  • We conclude that the difference in performance we’ve seen is probably just some random noise and that there’s probably no difference in performance.
  • We conclude that our result “is not statistically significant”.
• If 5% or less of our randomly generated differences in conversion rates are greater than or equal to our observed experiment result of ~+16.7%, then we say that our experiment result “is special enough”.
  • We conclude that our experiment result is unlikely to be random noise and that there’s enough evidence that the variant algorithm performs better than our control algorithm.
  • We conclude that our result is statistically significant.

Let’s see the above paragraphs in action. Where do our experiment results lie in our distribution of random noise?

plot_hist(simulated_diffs_in_rates,
          bins=15,
          observed_rate=0.167,
          title="Our range of pure randomness")

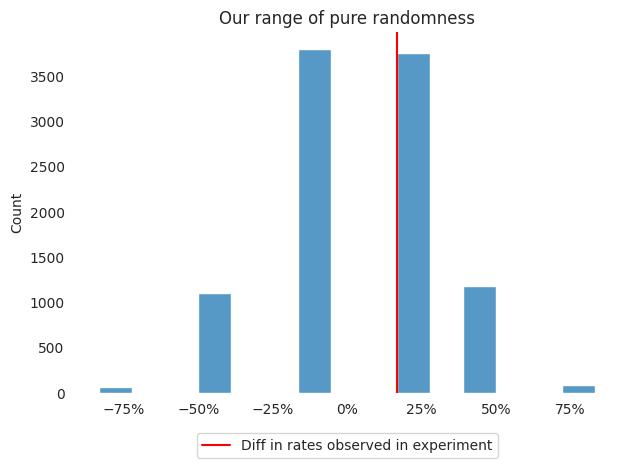
Looking to the right of our red line, we can see the observations that are greater than or equal to our observed result of ~+16.7%. It already looks like more than 5% of our randomly generated differences in conversion rates are >= ~+16.7%. But let’s confirm!

OBSERVED_DIFF_IN_RATES = 0.167 # this is our experiment result

num_diffs_gte_observed = (simulated_diffs_in_rates >= OBSERVED_DIFF_IN_RATES).sum()
num_samples = simulated_diffs_in_rates.shape[0]

print(f"{num_diffs_gte_observed:,} out of {num_samples:,} random samples show differences in rates greater than or equal to {OBSERVED_DIFF_IN_RATES:.1%}")
print(f"percentage of random noise distribution with difference in rates greater than or equal to {OBSERVED_DIFF_IN_RATES:.1%}: {num_diffs_gte_observed / num_samples:.2%}")

1,267 out of 10,000 random samples show differences in rates greater than or equal to 16.7%
percentage of random noise distribution with difference in rates greater than or equal to 16.7%: 12.67%

Now to conclude:

• ~12.67% of our random samples are greater than or equal to our observed experiment result of ~+16.7%
• We hoped that 5% or less of our random samples would be greater than or equal to our observed experiment result of ~+16.7%.
• Our experiment result “isn’t special enough”. In other words, our result “is not statistically significant”.
• Given how we’ve set up our experiment, our result is probably due to random noise.
• We don’t have enough evidence to say that our variant algorithm performs better than our control algorithm.

Nice!

An example where our results are “special enough”

To wrap this up, let’s simulate an example where the difference in performance is “special enough” and we therefore conclude that our variant algorithm might perform better than our control algorithm.

Let’s create a larger fake experiment:

NUM_CONTROL_USERS = 1_000_000
NUM_CONVERTING_CONTROL_USERS = 26_000

NUM_VARIANT_USERS = 1_000_000
NUM_CONVERTING_VARIANT_USERS = 26_400

# create our arrays of users
control_users = np.zeros(NUM_CONTROL_USERS)
control_users[:NUM_CONVERTING_CONTROL_USERS] = 1.0
control_conversion_rate = control_users.mean()

variant_users = np.zeros(NUM_VARIANT_USERS)
variant_users[:NUM_CONVERTING_VARIANT_USERS] = 1.0
variant_conversion_rate = variant_users.mean()

# calculate our experiment result
observed_diff_in_rates = variant_conversion_rate - control_conversion_rate

# chuck our users into a bag
all_users = np.hstack([control_users, variant_users])

print(f"control conversion rate = {control_conversion_rate:.2%}")
print(f"variant conversion rate = {variant_conversion_rate:.2%}")
print(f"observed absolute difference in conversion rates = {observed_diff_in_rates:.2%}")
print(f"observed relative difference in conversion rates = {observed_diff_in_rates / control_conversion_rate:.2%}")

control conversion rate = 2.60%
variant conversion rate = 2.64%
observed absolute difference in conversion rates = 0.04%
observed relative difference in conversion rates = 1.54%

We’ll use the numba library to do the resampling efficiently:

@njit(parallel=True)
def sample_diffs_in_rates(all_users, num_control_users, num_simulations):
    results = np.zeros(num_simulations)
    for i in prange(num_simulations):
        # numpy random shuffling appears to be slower when using numba
        random.shuffle(all_users)
        control_rate = all_users[:num_control_users].mean()
        # we assume the rest of the users are variant users
        variant_rate = all_users[num_control_users:].mean()
        results[i] = variant_rate - control_rate
    return results

Run the simulations!

NUM_SIMULATIONS = 10_000

sampled_diffs = sample_diffs_in_rates(all_users, NUM_CONTROL_USERS, NUM_SIMULATIONS)

Let’s look at where our observed difference of 0.04% lies in our range of randomness:

plot_hist(sampled_diffs,
          bins=50,
          observed_rate=observed_diff_in_rates,
          title="Our range of pure randomness")

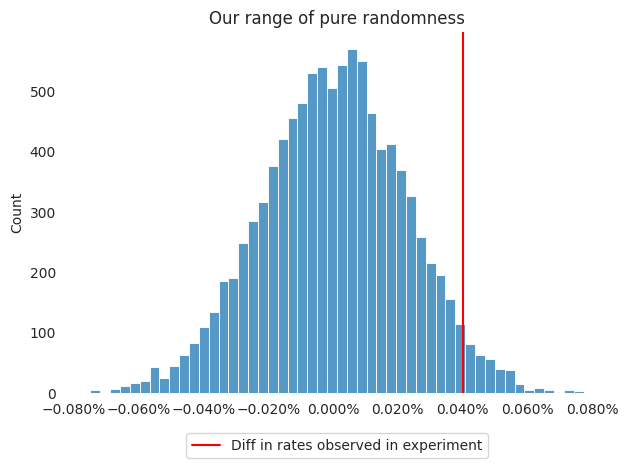
Given our “specialness threshold” of 5%, how well does randomness describe our experiment results?

sampling_specialness_result = (sampled_diffs >= observed_diff_in_rates).sum() / sampled_diffs.shape[0]
print(f"sampled 'specialness' result: {sampling_specialness_result:.2%}")

sampled 'specialness' result: 3.41%

That’s less than 5%! We have a special, statistically significant result. Our variant algorithm probably performs better than our control one.

Let’s compare this to the “actual” result as derived through traditional statistics:

actual_specialness_result = score_test_proportions_2indep(NUM_CONVERTING_VARIANT_USERS, NUM_VARIANT_USERS, NUM_CONVERTING_CONTROL_USERS, NUM_CONTROL_USERS, alternative="larger")
print(f"actual 'specialness' result: {actual_specialness_result.pvalue:.2%}")

actual 'specialness' result: 3.83%

We also have a statistically significant result.

The “specialness” values aren’t equal because they’re derived in different ways. However, they’re close enough for the day-to-day of data scientists. What’s more important is that you specify your “specialness threshold” before running an experiment and stick to it when making decisions based on your experiment’s results.

A note for if you’re doing this at work

You shouldn’t implement this stuff from scratch. Use a robust implementation like the one in scipy.

Phew! We’re done!

Justin